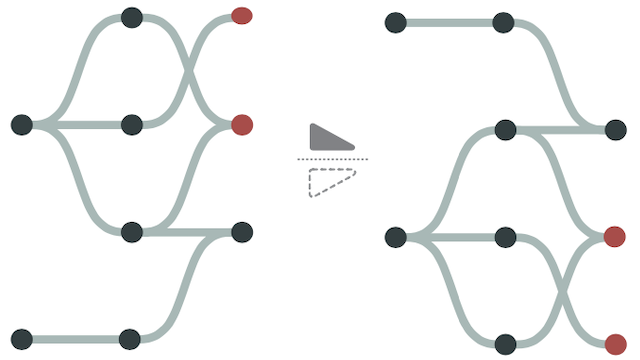
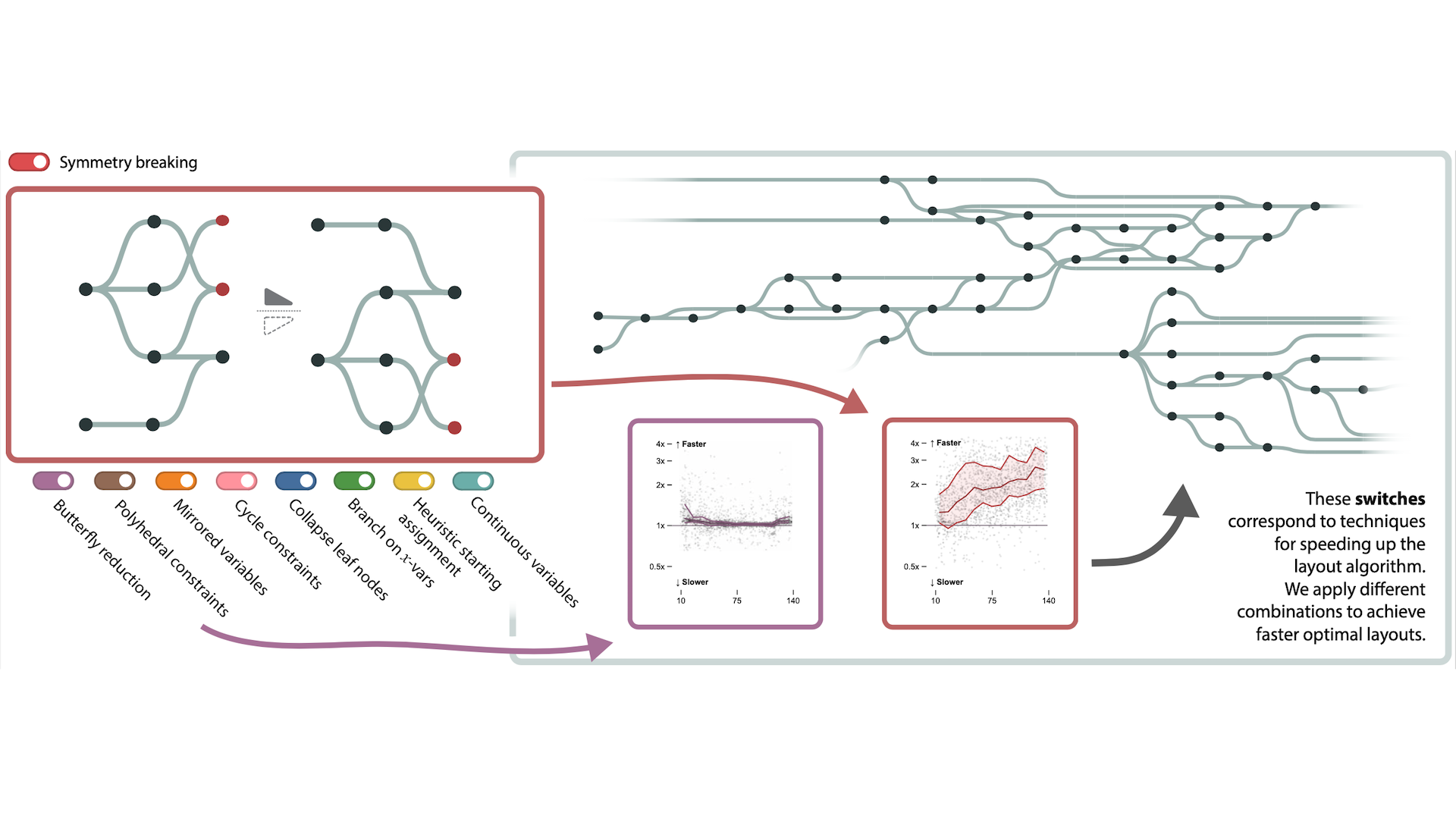
A layered graph is an important category of graph in which every node is assigned to a layer, and layers are drawn as parallel or radial lines. They are commonly used to display temporal data or hierarchical graphs. Previous research has demonstrated that minimizing edge crossings is the most important criterion to consider when looking to improve the readability of such graphs. While heuristic approaches exist for crossing minimization, we are interested in optimal approaches to the problem that prioritize human readability over computational scalability. We aim to improve the usefulness and applicability of such optimal methods by understanding and improving their scalability to larger graphs. This paper categorizes and evaluates the state-of-the-art linear programming formulations for exact crossing minimization and describes nine new and existing techniques that could plausibly accelerate the optimization algorithm. Through a computational evaluation, we explore each technique's effect on calculation time and how the techniques assist or inhibit one another, allowing researchers and practitioners to adapt them to the characteristics of their graphs. Our best-performing techniques yielded a median improvement of 2.5-17x depending on the solver used, giving us the capability to create optimal layouts faster and for larger graphs. We provide an open-source implementation of our methodology in Python, where users can pick which combination of techniques to enable according to their use case. A free copy of this paper and all supplemental materials, datasets used, and source code are available at https://osf.io/5vq79.